Quantum computing for QCD
In the last few years, rapid advances in quantum devices have led to an explosion of interest in quantum computing. The basic idea of quantum computing is that by cleverly programming “quantum bits” to take advantage of quantum superposition and entanglement, one can exploit complex many-body quantum correlations in order to solve certain otherwise intractable computational problems. While it is not yet clear exactly which problems could be solved, or to what extent these quantum devices will continue to improve, there is good cause to speculate that they may one day revolutionize many aspects of science and technology.
I am interested in a particular class of problems known as quantum simulation; that is, simulating the dynamics of a quantum mechanical system. With traditional computers, the time needed to simulate a many-body quantum system – for example the propagation of probes through nuclear matter – scales exponentially in the size of the system. Simulating a system with as few as 100 particles would be impossible. Quantum computers, on the other hand, can evolve quantum systems naturally in polynomial time – a savings that can bring the cost down from “longer than the age of the universe” to “a few minutes.”

What is less known, however, is the extent to which quantum advantage holds for quantum field theory. We know that the dynamics of QCD cannot be simulated efficiently on classical computers – lattice QCD methods encounter numerically intractable integrals when trying to solve real-time dynamics. And it has been shown that it is possible to simulate simple field theories efficiently. But it remains unknown whether QCD – the most complex theory in particle physics – is efficiently simulatable by a quantum computer. If possible, this would revolutionize our understanding of QCD, allowing us even to make real-time movies of the hadronization process that binds quarks and gluons into protons. If it turns out to not be possible, this would be arguably even more interesting: it would demonstrate a violation of a deep conjecture in computer science known as the Quantum Extended Church-Turing Thesis. This would mean that nature realizes a system of unprecedented computational complexity, and one could dream of using a “QCD computer” to efficiently solve problems that neither classical nor quantum computers can, such as NP-hard problems.
My research has focused on open quantum systems, in which a subsystem interacts with an external environment. While the language of open quantum systems has not traditionally been used in the field of QCD, it is in fact a rather natural language to describe probes, such as jets or heavy quarks, traversing the quark-gluon plasma – since we are interested to understand how these probes are modified. And importantly, such a formulation is amenable to quantum simulation.
One natural use case of open quantum systems is the evolution of quarkonia in the quark-gluon plasma. Quarkonia can be described with non-relativistic QCD, which simplifies its use for quantum simulation since a full quantum field theoretical treatment is not needed. My colleagues and I formulated a way to simulate this and other similar systems on a quantum computer and performed proof-of-principle demonstrations on IBM’s quantum hardware [1]. This was the first application of quantum computing to hard probes in the quark-gluon plasma, and was covered by Symmetry Magazine.
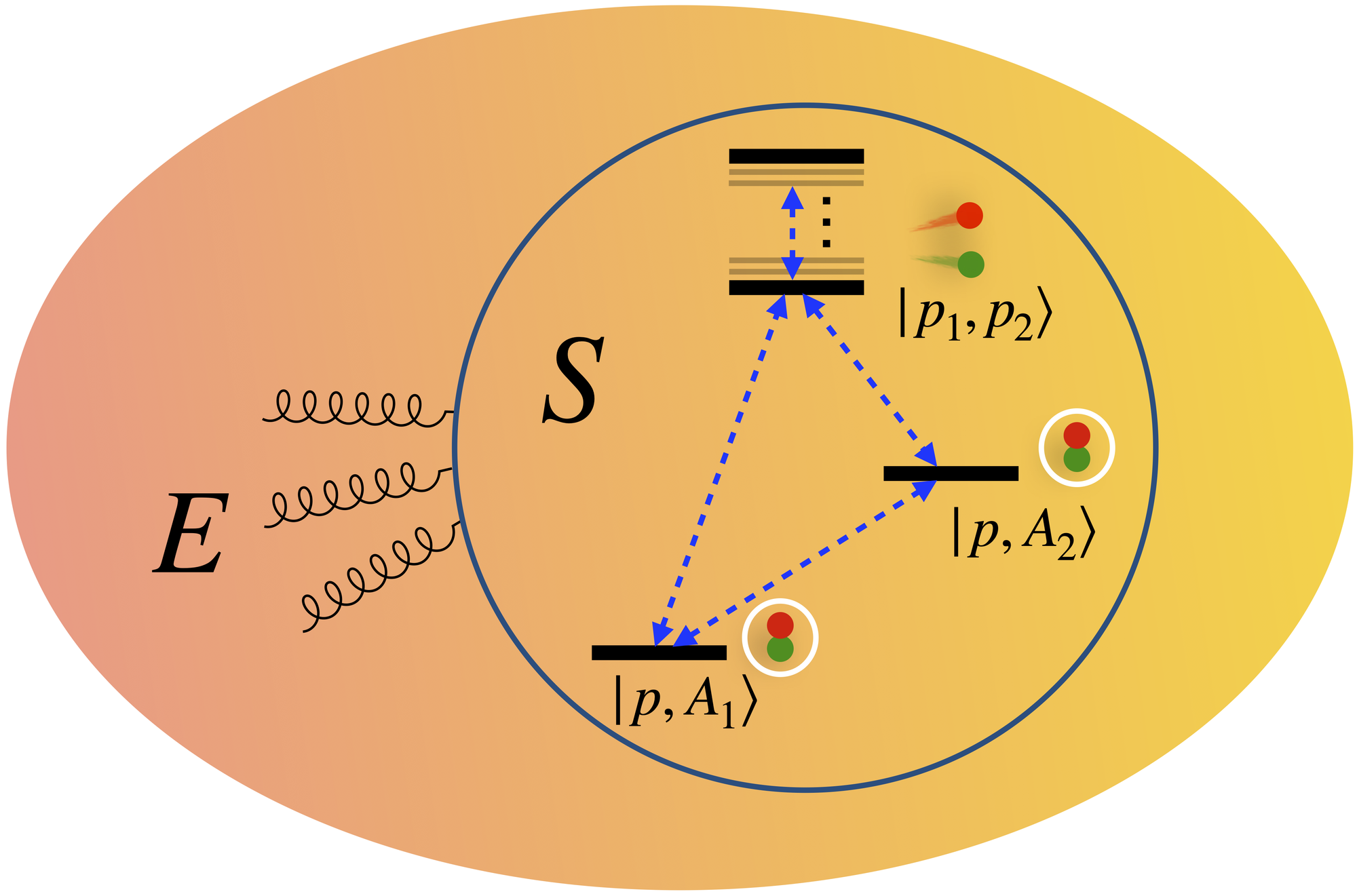
Since then, my colleagues and I have shifted focus to explore the simulation of quantum field theories. We have concentrated on a simpler theory called the Schwinger model, which allows us to explore the subtleties of quantum simulation of field theories while still retaining QCD-like features such as confinement. We recently formulated a method to simulate non-equilibrium dynamics in the Schwinger model [2] and have simulated the real-time dynamics of a key hadronization mechanism from first principles [3].
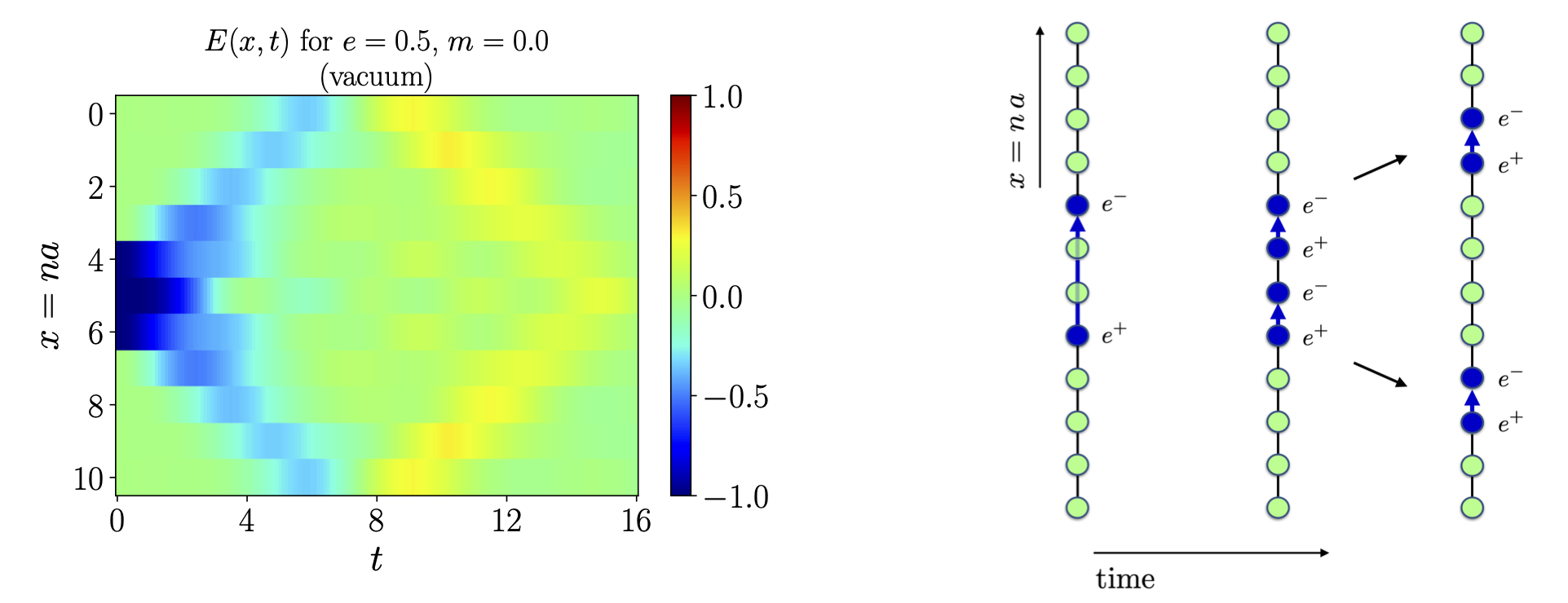
Ultimately, simulating full QCD will require scalable quantum error correction, which may not arrive anytime soon. However, the advent of near-term quantum devices and the rapid pace of growth gives hope that from any point on – it could be ten years, or it could be next year – we will find real-world applications of quantum computing for fundamental science. I currently organize the QC-HEP Seminar Series to bring high energy and nuclear physicists together with quantum computing experts in order to confront this open challenge.